HISTOGRAMA

O Histograma é aplicado quando você necessitar encontrar e mostrar uma distribuição de dados por gráfico de barras com certo número de unidades por cada categoria.

Como já vimos no diagrama de Pareto, é de grande auxílio visualizar na forma de um gráfico de barras a frequência com que certos eventos ocorrem (distribuição de frequência).

O diagrama de Pareto por seu turno, trata apenas de características de um produto ou serviço, isto é, o tipo de defeito, o problema, riscos etc. (os seus atributos).

Um histograma envolve a medição de dados, tais como, temperatura, dimensões etc. e, mostra sua distribuição.

Isto é crítico, pois sabemos que todos os eventos repetitivos produzirão resultados que variam com o tempo.

Um Histograma revela quanto de variação existe em qualquer processo.

Após pronto, considere, além da forma de distribuição:

a) Se a curva está atendendo a especificação. Se não, quanto da curva está fora? (variabilidade).

b) Se a curva está centrada. A maioria dos itens está acumulada à direita ou à esquerda? (inclinação).

Vamos construir um exemplo, para que você possa associar ao aplicar aí na sua organização.

Segue os dados coletados de uma amostra de medidas de diâmetros de furos (em milímetros) em uma placa. A especificação para o diâmetro de furo é de 8,8 a 9,3 mm, com média = 9,05 mm.

Criei esse exemplo em uma planilha do Excel:

1o. Contar a quantidade de dados coletados na amostra.

Em nosso exemplo, estamos com 59 leituras (n = 59).

2o. Calcular a amplitude R.

R = (Maior valor da amostra – Menor valor da amostra) = 10,2 – 7,8 = 2,4

3o. Dividir a amplitude em classes (K).

Use a tabela abaixo para escolher o valor de K. Essa tabela fornece uma indicação aproximada para determinação aproximada da quantidade de classes.

Vamos escolher 6 classes. K = 6.

4o. Determinar o intervalo de classe (H).

Use a fórmula: H = R / K

H = 2,4 / 6 H = 0,4

Se o resultado for um número “quebrado”, por exemplo 0,38 arredonde para uma casa decimal acima.

5o. Determinar o limite da classe.

Esse limite da classe é o passo entre as classes. Para isso, pegue o menor valor coletado da amostra (= 7,8). Em seguida, adicione o valor do intervalo de classe (= 0,4) e assim teremos 8,2.

Para a primeira classe estamos com o o intervalo entre 7,8 e 8,2.

E, limite inferior da próxima classe será também 8,2.

Para ajustar, vamos assumir que o limite inferior da 1a. classe será 8,1. Pois, os limites entre classes não podem ser os mesmos.

A 1a. classe ficará: limite inferior = 7,8 e limite superior = 8,1.

A 2a. classe ficará: limite inferior = 8,2 e limite superior = 8,2 + 0,4 = 8,6 e faremos o mesmo ajuste da 1a. classe, ou seja, os limites da 2a. classe serão: 8,2 e 8,5.

Com isso, cada uma das classes serão mutuamente exclusivas.

Continuemos a montar as classes até o limite K, acima calculado (K = 6).

6o. Vamos construir a tabela de frequências baseadas nos valores, conforme demonstrado acima.

7o. Com a tabela acima definida, podemos construir o Histograma de nosso exemplo.

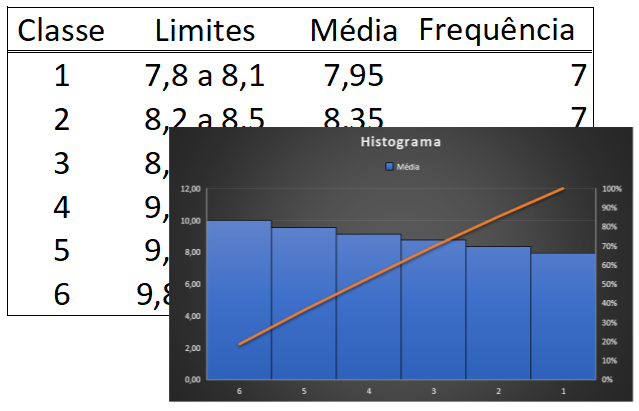
Se estiver a montar a sua na planilha de Excel, escolha a tabela acima; vá em “Inserir”; no menu escolha “Gráficos Recomendados”; clique na aba “Todos os gráficos” e escolha “Histograma”. Aqui optei pela segunda opção (Pareto).

COMENTÁRIOS

A. Histograma é ferramenta importante ao permitir uma visão geral da variação em um conjunto de dados coletados.

B. No exemplo, nota-se que a uma tendência junto a classe 3 (8,6 a 8,9). E, também, porém menor, nas classes 5 (9,4 a 9,7) e 6 (9,8 a 10,2). Isso indica que o processo de furar necessita ser corrigido e melhorado, pois está a gerar resultados diferentes do especificado, com forte tendência a furos maiores.

C. VARIABILIDADE e INCLINAÇÃO.

VARIABILIDADE indica se os resultados coletados variam de pequena (próximos ao especificado) a grande (dispersos em relação ao especificado).

Em nosso exemplo pode-se afirmar que a Variabilidade é pouca.

INCLINAÇÃO indica se os resultados coletados estão Positivamente inclinados (Tendem a ir da esquerda para a direita, com diminuição) ou Negativamente inclinados (tendem a ir da esquerda para a direita, com diminuição).

Na figura do gráfico escolhida (Pareto) essa inclinação está invertida. Portanto Negativa, o que indica que a uma tendência dos resultados aumentarem em relação ao especificado, se não houver nenhuma ação corretiva.

Considere aplicar o Histograma em seus processos produtivos e operacionais, para medir, acompanhar e treinar seus profissionais, de maneira a agirem, em caso de alterações nos resultados que diferem do especificado e podem gerar desperdícios e perdas.

Avante sempre, syn!